Se mettre en orbite autour de Mars

Bonjour si on envoie une sonde se mettre en orbite autour de mars est t'il plus facile de se mettre en orbite autour de mars dans le sens de sa rotation sur elle même où l'inverse? Merci!

Non ça ne change rien

Oui ; ça ne change que si on part du sol de la planète, car dans le sens de sa rotation on bénéficie de l'effet de fronde qui fait gagner de la vitesse au lanceur.

bonjour
il serait bien de mettre un titre plus explicite par se que Mars.... c'est large

mars comme la terre tourne autour de la terre sur une orbite prograde (direct , sens inverse des aiguilles d'une montre vu depuis au dessus du pole nord) , de plus c'est deux planètes sur elle même aussi dans le sens prograde
pour une sonde venant de la terre (donc après un vol héliocentrique) la différence entre les deux sens est négligeable. il est légèrement plus simple de se mettre sur une orbite prograde (même sens que la planète) car on peut conserve une orbite de transfert passent "d'en dessous" de la planète, mais si on veut être en rétrograde, il faudrait passer au dessus. mais vu la taille de la planète comparé au trajet, une différence de vitesse infime au départ permet de passer au dessus ou en dessous.(pas sur d’être compréhensible)

par contre pour mettre un objet en orbite depuis la surface de mars, les chose sont beaucoup plus claire. vu que mars tourne sur elle même relativement vite (comme la terre) on a gratuitement une vitesse prograde qu'on a pas besoin de fournire. par contre si on veut partir en retrograde, il faut déjà annulé cette vitesse puis fournir toute la vitesse de mise en orbite.

phenix a écrit:bonjour
il serait bien de mettre un titre plus explicite parce que Mars.... c'est large

Exact. Mieux comme ça ?

Si j'ai bien compris la différence de vitesse a procuré a la sonde pour la ralentir et la mettre en orbite soit prograde ou rétrograde vient de la vitesse donner au départ de la terre?

Alors là vitesse orbital autour de mars d'une sonde qui serait sur une orbite circulaire a 200 km de hauteur est la même que si elle est sur une orbite prograde ou rétrograde?

Yomaha a écrit:Alors là vitesse orbital autour de mars d'une sonde qui serait sur une orbite circulaire a 200 km de hauteur est la même que si elle est sur une orbite prograde ou rétrograde?

Oui. la vitesse en un point de l'orbite se calcule ainsi
mu est un paramètre qui dépend uniquement de la masse de la planète
R est la distance entre le centre de la planète et la sonde 
a est la moyenne entre la plus grande et la plus petite distance séparent la sonde du centre de la plante au cours d'une orbite. 


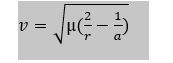
la vitesse de rotation de la planète d'intervient nul part une fois en orbite (elle intervient au décollage)

Connaissez vous un site qui explique comment résoudre cette équation?

resoudre? il n'y a pas de resolution juste un calcul

exemple prenons MRO :https://fr.wikipedia.org/wiki/Mars_Reconnaissance_Orbiter

on sais que l'apoastre (point ou MRO s'eloigne le plus de mars) est a 316km d'altitude (distance avec la surface) et le periastre (point le plus bas) a 250km

les altitude ne sont pas intéressent en mécanique orbitale , il faut connaitre le rayon  (la distance entre le centre de gravité de la planete et celui de la sonde). 
on sais que le rayon de la surface est égale a 3 396,2km donc:
rayon periastre=250+3 396,2= 3656,2km
rayon apoastre=3712,2km

la valeur "a" le demi-grand axe est la moyenne de c'est deux valeur donc a=(3656,2+ 3712,2) / 2   =3684,2km

pour trouvé mu, on la trouve sur internet, le mieux c'est de le gardé en km3/s²
https://fr.wikipedia.org/wiki/Param%C3%A8tre_gravitationnel_standard
pour mars , c'est 42 828 km3/s²

donc on cherche la vitesse pour une altitude de 300km , donc un rayon "r" de 3696,2km

donc

v=racine(mu (2/r  - 1/a))= racine(42 828 (2/3696,2 - 1/3684,2)) = 3,398 km/s

sa tombe bien, je suis entraîne de préparé un site sur l'exploration de venus et j'ai "accidentellement" redigé une sorte de minicours de meca orbital, j'avais prévu de publier le word de se cours se soir ou demain.

Yomaha a écrit:Bonjour si on envoie une sonde se mettre en orbite autour de mars est t'il plus facile de se mettre en orbite autour de mars dans le sens de sa rotation sur elle même où l'inverse? Merci!

Effectivement, les réponses ont été données et même la formule qui donne la vitesse orbitale.
J'ajouterai que, en général, le voyage vers Mars se fait en suivant une trajectoire (proche de Hohmann) qui ralentit au niveau de l'orbite de Mars (aphélie) et qui, en l'absence de Mars, amènerait la sonde à revenir vers une orbite héliocentrique plus basse (périhélie).
Autrement dit, au niveau de Mars, la sonde va moins vite que Mars. Sachant cela, pour rencontrer Mars, la stratégie consiste à envoyer la sonde légèrement devant Mars et comme Mars va plus vite autour du soleil que la sonde, elle rattrape la sonde avec un différentiel de vitesse relativement faible.
Il faut bien entendu que la sonde soit un peu décalée pour ne pas tomber sur Mars et effectuer une manoeuvre d'insertion orbitale pour éviter de tourner autour et de repartir dans le système solaire.

Bonjour une sonde partant de la terre et voulant se mettre en orbite autour de mars doit ralentir de quelle vitesse environ rendu sur place?merci

Tout dépend de l'orbite visée, mais grosso modo, entre 0.8km/sec et 2km/sec.
Plus l'altitude de l'orbite est grande ou elliptique, moins grande sera la vitesse a annuler.
En revanche plus l'orbite est basse et circulaire plus grande sera la vitesse a annuler.

Voici quelques exemple:

Mars Odyssey: 400 km x 400 km dV= ~2.08km/sec
MAVEN: 150 km x 5000 km dV= ~1.46km/sec
Mars Express: 298 km x 10 017 km dV= ~1.23km/sec
Viking1: 350 km x 56 000 km dV= ~0.83km/sec
Mars Orbiter Mission: 427 km x 78 500 km dV= ~0.79km/sec

Il est intéressant de noter, à cette occasion, qu'il peut être plus efficace de freiner au plus bas pour fixer l'apoaps, pour profiter de l'effet Oberth, avant de rehausser à nouveau le périaps à l'altitude souhaitée. Cela n'ira tout de même pas jusqu'à équivaloir une orbite circulaire haute dès le départ, selon les altitudes considérées !

Par exemple : 500*500, cela peut peut être valoir le coup de décélérer non pas à 500km à l'arrivée, mais plutôt à 100km, au plus bas du puit gravitationnel, de fixer l'apoaps à 500km, puis de rehausser le périaps à 500km.

En revanche, il me semble peu probable qu'une orbite circulaire lointaine de 10000*10000km suive cette logique, et une décélération directement à 10000km pour circularisation sera sans doute plus économe qu'une double manoeuvre.

Tout cela se calcule, bien sur ! Je ne sais plus de combien est le rapport de changement d'altitude qui rend une manoeuvre bi-elliptique plus intéressante, mais c'était quelque chose comme 13, je crois... #vague.

Yomaha a écrit:Bonjour une sonde partant de la terre et voulant se mettre en orbite autour de mars doit ralentir de quelle vitesse environ rendu sur place?merci

si tu veut le calculé toi-meme , c'est plus simple qu'il n'y parait, voici un lien vers une intro a la mecanique orbtial
http://www.k-upload.fr/afficher-fichier-2019-02-06-1d7871699mecaorbital.docx.html

a la fin du chapitre DV il y a un exemple d'application numérique mais pour un voyage mais vers  une planète plus intéréssente que Mars Vénus . si tu prend les donnée de mars a la place de Vénus et que tu inverse les Dv d'hohmann (Dv1 pour la terre et Dv2 pour mars) tu devrait tombé sur se que tu cherche

PS: si quelqu'un a un commentaire sur ce document, n’hésité pas a le partagé ici :ven:
http://www.forum-conquete-spatiale.fr/t20233-venautics-futur-site-sur-l-exploration-de-venus?highlight=venautics

Est t'il plus facile de se mettre en orbite autour d'une planète plus qu'elle est massive?

Bah c'est une bonne question ça, tient ! Si l'on prend l'exacte orbite de Mars, par exemple, et qu'on la remplace par Venus / Jupiter / une autre planète avec des caractéristiques données.

En première approche j'aurai dit que oui, plus massive ==> vitesse orbitale plus importante (à iso distance au centre de masse, pas iso altitude ^^), mais d'une certaine manière lorsqu'on croire une planète depuis un transfert d'Hohmann, il faut "freiner" au periaps pour ne pas être catapulter et se mettre en orbite, circulariser. Cela signifierait qu'une vitesse orbitale élevée, correspondrait à un DeltaV moindre pour freiner.

Tout cela sans prendre en considération l'Effet Oberth qui, à nouveau, serait plus important dans un puit gravitationnel plus profond, permettant un bénéfice sur travail mécanique du burn rétrograde d'arrivée.

Mais intuitivement je dirais qu'il reste pourtant plus difficile de se mettre en orbite d'un corps plus massif. Sans doute parce que l'accroissement de la vitesse, par interaction gravitationnelle lorsqu'on parvient au voisinage, sera simplement plus important que les deux gains évoqués précédemment !

En somme, la vitesse d'approche sera la même, car même trajectoire, mais l'accroissement de vitesse lié à la chute dans le puit, sera plus élevé avec un corps plus massif, et il faudra donc dépenser plus d'énergie dissiper la vitesse relative nécessaire la mise en orbite.

question interente, calculons

la vitesse au periastre d'un objet venant d'une orbite héliocentrique se calcul ainsi

Vp=racine( 2*G*M/rp   +vinf²)    G la constante de gravitation , M la masse de l'astre,  rp le rayon (distence entre le centre de la planete et l'objet) et Vinf la vitesse a laquelle l'objet rentre dans le sphere d'influence de la planete (en gros)

la vitesse de l'orbite circulaire est egale a 
Vo=racine(G*M/r)

si on veut passé de la trajectoire hyperobolique a l'orbite circulaire, il faut que freinage de :
Dv=Vp-Vo=racine (2*G*M/rp  +vinf²)    - racine (G*M/rp)

donc il faut s’intéressé a la relation M/rp. en tout logique on prend un rayon au periastre le plus bas possible , donc on vas simplifier en disant que Rp est egale au rayon de la planete . or la masse de la planete est egale a sa masse volumique sont volume, le volume vos pi*R*R*R
donc
M/R ~ ro*pi*R*R*R/R=ro*pi*R²

donc plus une planète est grande , plus M/R est important (de plus  a composition similaire, la masse volumique augmente avec le volume car les materiau au centre sont plus dense). donc G*M/R aussi 
or se facteur G*M/R est multiplié par 2 dans la racine du calcule de la vitesse au periaste, mais pas dans la vitesse de l'orbite circulaire , 






Par contre si on ne souhaite pas se mettre sur une orbite circulaire mais juste rester autour de la planete , il faut juste qu'au periastre la vitesse soit inférieur a la vitesse de liberation qui est 
Vl=racine(2 *G*M/rp)

Dv>racine (2*G*M/rp   +vinf²)     -  racine(2*G*M/rp)

comme on l'a vu 2*G*M/Rp augmente avec si la taille de la planete augmente, donc plus la planete est important moins l'influence de vinf² est faible    donc le Dv faible.



donc pour conclure. si le but est simplement de se faire capture est de se mettre sur une orbite très elliptique le mieux est une grosse planete , parcontre plus on se rapproche d'une orbite circulaire plus on a interet a avoir une petite planète

Bonjour une trajectoire pour aller sur mars en 260 jours s'appelle un transfert de type hohmann mais souvent sur internet ils parlent d'aller sur mars en 180 jours alors qu'elle type de trajectoire il utiliserait? Et prendrait t'elle plus de carburant a l'arrivée?

Yomaha a écrit:Bonjour une trajectoire pour aller sur mars en 260 jours s'appelle un transfert de type hohmann mais souvent sur internet ils parlent d'aller sur mars en 180 jours alors qu'elle type de trajectoire il utiliserait? Et prendrait t'elle plus de carburant a l'arrivée?

l'orbite de hohmann signifie simplement qu'on place le point de depart au periastre et le point d'arrivé a l'apoastre (si le départ est plus proche du soleil que l'arrivé). donc c'est le trajet a énergie minimal entre les deux points.


dans notre cas: en bleu l'orbite de la terre, en rouge celle de mars et en jaune l'orbite de transfert

donc le temps de trajet est égal a la moitié de la période de l'orbite.

si on veut aller plus vite il faut rehaussé l'apoastre , car un objet vas plus vite proche de sont périastre, de plus , cela réduit la distance. Donc la distance sera parcouru uniquement avec la portion la plus rapide et permet un gain de temps au prix d'une plus grand vitesse initiale (donc le cout en ergol) mais aussi final (donc la quantité d'ergole pour freiner ou la vitesse a laquelle la sonde rentre dans l’atmosphère).

Mais si on met le periastre autour du soleil derrière la terre au départ en changeant l'angle d'éjection de l'orbite terrestre la distance a parcourir va être plus courte sans a avoir a rehausser l' apoastre plus haut que l'orbite de mars (je suis pas sûr que c'est compréhensible)

j'avoue que je ne vois pas se que tu veux dire, un petit schema aiderai peut etre (il es possible d'en faire un sur paint et de le coller ici grâce a la disquette devant la photo , sous le aucune en haut quand tu ecrit).

Ce que je voulais expliquer est la deuxieme image (la terre est caché par les points d'interrogation.)

Ah KSP, le meilleur des prof de mécanique orbital :ven:

non c'est moins rentable d'abaisse le périastre que de monté l'apoastre.
on vas plus vite au niveau du périastre et moins vite au niveau de l'apoastre. or si on diminue le peri sans touché a l'apo, sa veut dire qu'on utilisera la portion la moins rapide de l'orbite . au contraire si on monte l'apo sa veut dire qu'on rejoindra mars avant de passer dans la portion lente pres de l'apo.

J'ai fait des calculs pour un trajet terre-Vénus (mes fichiers de calcul sont calibre pour l'exploration de venus)  
un transfert de hohmann prend 144,15jours
si on rehause l'apo de 1millions de km sa prend 129jours
si on abaise le peri de 1 millions de km sa prend 132 jours